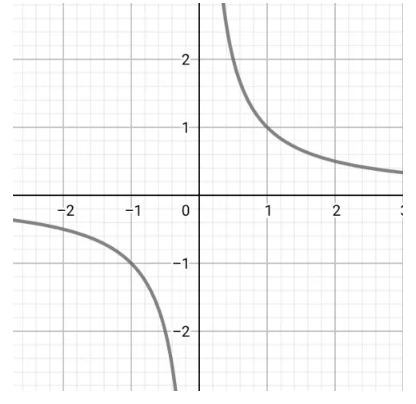
求函数定义域的方法如下:
①整式:若y=f(x)为整式,则函数的定义域是实数集R.
②分式:若y=f(x)为分式,则函数的定义域为使分母不为0的实数集.
③偶次根式:若y=f(x)为偶次根式,则函数的定义域为被开方数非负的实数集.
④X0(x≠0)
⑤对数函数真数大于零
⑥几部分组成:若y=f(x)是亏兆档由几部分数学式子的和、差、积、商组成的形式,定义域是使各部分都有意义的集合的交集.
⑦实际问题:若y=f(x)是由实际问题确定的,其定义域要受实际问题的约束.
函数的定义域是我们上了高中后接触到的新的名词,其实相关知识我们早有接触,其实它就是我们之前学习函数中自变量x的取值范围,到了高中我们将这个取值范围定义为函数的定义域。
那如何理解定义域呢?数学总是抽象难理解的,函数更上如此,所以相当一部分同学听到函数就头皮发麻。
所以为了了解抽象的定义域我先从具体的事例开始说明。比如人类的活动区域可以视为一个定义域,具体指地球上的陆地部分(有人会觉得我们有时候会去水里游泳呀,等等不一定一直在陆地,emmm我要讲的一个意思是人类是陆生动物,日常生活都在陆地上销乱进行,如果长时间待在水里将死亡),那么鸟类活动区域的定义域就是陆地与天空,相比与人类它的定义域更大....
函数定义猜陪域:数学名词,是函数的三要素(定义域、值域、对应法则)之一,对应法则的作用对象。指函数自变量的取值范围,即对于两个存在函数对应关系的非空集合D、M,集合D中的任意一个数,在集合M中都有且仅有一个确定的数与之对应,则集合D称为函数定义域。