Simone
∴AP=t（cm），PD=AD-AP=24-t（cm），CQ=3t（cm），BQ=BC-CQ=26-3t（cm），
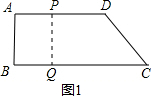
（1）如图1：∵AD∥BC，
∴当PA=BQ时，四边形ABQP是平行四边形，
∵∠B=90°，
∴四边形ABQP是矩形，
即t=26-3t，
解得：t=6.5，
∴t=6.5s时，四边形ABQP是矩形，
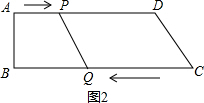
（2）∵AD∥BC，
∴当QC=PD时，四边形PQCD是羡掘平行四边形．
此时有3t=24-t，
解得t=6．
∴当t=6s时，四边形PQCD是平行四边形．
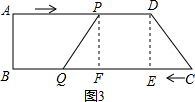
（3）当四边形PQCD为等腰梯丛慧形时，如图所示：
在Rt△PQF和Rt△CDE中，
∵PQ=DC，PF=DE，
∴Rt△PQF≌Rt△CDE（HL），
∴QF=CE，
∴QC-PD=QC-EF=QF+EC=2CE，即3t-（24-t）=4
解得：兄郑核t=7（s）
即当t=7（s）时，四边形PQCD为等腰梯形．
