转动惯量乘以角加速度是表示转动刚体的动量矩。
平动中的牛顿第二定律:F = ma,合外力 = 质量 × 线加速度高颤颤。转动中,就成了 M = I β;合外力矩 = 转动惯量 × 角加速度。
平动中,牛戚败顿第二定律的动量表述:合外力 = 线动量的变化率;线动量 = 质量 × 速度。转动中,牛顿第二定律的角动量表述:合外力矩 = 角动量的变化率;角动量 = 转动惯量 × 角洞罩速度。
平动中的动能:Ek = ½ mv² = ½ 质量 × 线速率的平方。转动中的动能 Ek = ½ mv² = ½ 转动惯量 × 角速率的平方。
相关信息:
转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大小)无关。形状规则的匀质刚体,其转动惯量可直接用公式计算得到。
而对于不规则刚体或非均质刚体的转动惯量,一般通过实验的方法来进行测定,因而实验方法就显得十分重要。转动惯量应用于刚体各种运动的动力学计算中。
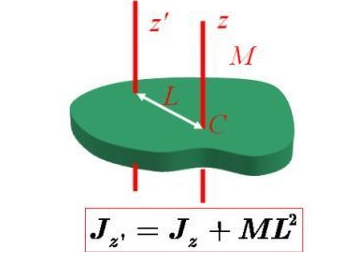
面积对于一轴的转动惯量,等于该面积对于同此轴平行并通过形心之轴的转动惯量加上该面积同两轴间距离平方的乘积。由于和式的第二项恒大于零,因此面积绕过形心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。