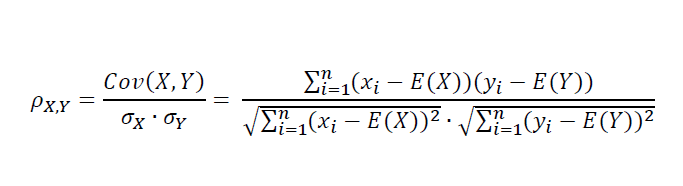对皮尔逊相关系数的理解可以从很多个角度来进行,有人从协方差矩阵的角度思考,有人从向量cosine夹角的角度思考,这几种方式只要能让你对皮尔逊相关有感性的理解就可以。我们假设两组数据X和Y,每个都包含n个元素,计算二者协方差的方法就可以记为
其中E(X)和E(Y)分别代表二者的期望,也就是平均值。我们看分子部分,在分子中,当总体的一个值小x比X的平均值大,而且小y也比Y的平均值大的时候,分子就是正的,或者二者都小于平均值的时候,分子也是正的。
当二者不都大于或者小于平均值的时候,分子就是负的。这里我们就可以感性的理解,如果数据杂乱,正负抵消,那么这个协方差就很小,就谈不上二者相关陵隐败;如果两个变量相关,整个协方差就是很大的正值或者负值。
然而从这里,我们也看出一些问题,就是这里面二者都是带有量纲的数据,假如说x都是0.01左右的数据,y都是1000左右的数据,那么整个的协方差就很容易被这么大的y带跑偏,为了解决这个量纲的问题,我们就消除量纲,从而得到一个无量纲的量,也就是皮尔逊携答相关系数了。
简介:
相关系数是衡量两个数据相关关系的指标,两个数据相关在某种程度上可以帮助人们理解事物的变化规律。例如在商品推荐中,我们已知一个用户A的购买喜好,同时发现另一个用户B的购买数据和A相关性很高,那么我们可以根据A的喜好去给B推荐相关的产品,等等。
皮尔逊相关系数(Pearson correlation coefficient)就是最为常用的用来衡量尺颤两个变量线性相关关系的指标,有了指标就有评分的依据,然而评分多高代表二者相关。