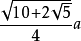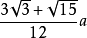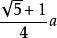如下图:
正二十面体由20个等边三角形所组成的正多面体,共有12个顶点,30条棱,20个面。为五个柏拉图多面体之一。各个面都是全等的正多边形,并且各个多面角都是全等汪键的多面角。其中面数最少的是正四面体。
体心到每个顶点的距离(外接球半径)=
体心到每个面的中心的距离(内切球半径)=
体心到每粗陵滚条棱的中点的距离(切棱球半径)=
性质:
1、正二十面体的外接球、岩余内切球、内棱切球都存在,并且三球球心重合。
2、正二十面体的外心、内心、内棱心重合的点称为该正二十面体的中心。
3、正二十面过任顶点和正多面体中心的直线必然经过正二十面体的另一顶点,并且这两个顶点到正二十面体中心的距离都相等。
4、连线经过正二十面体的中心的两点称为相对顶点,连两双相对顶点的两条棱称为正二十面体的对棱,由对棱围成的两个面称为正二十面体的对面。
5、正二十面体的对棱、对面都平行。