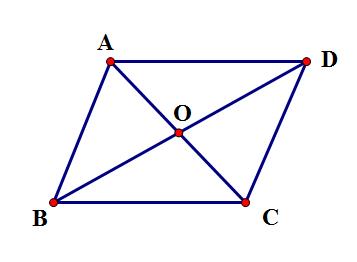
Simone【对角线互相平分的四边形是平行四边形】
设四边形ABCD的对角线AC和BD交于O，OA=OC，OB=OD，求证：四边形ABCD是平行四边形。
证明：森禅
∵在△AOD和△COB中，
OA=OC，运春含
∠AOD=∠COB（对顶角相等），
OB=OD，
∴△AOD≌△COB（SAS），
∴∠OAD=∠OCB，
∴AD//BC（内错角相等，两直线平行），
同理：△AOB≌△COD（SAS），
∴∠ABO=∠CDO，
∴AB//CD（内错角相等，两直线平行）
∴四边形ABCD是平行四边形（平行四边形定旁笑义：两组对边分别平行的四边形是平行四边形）。
