两者都是表征使物体发生旋转的能力的物理量。计算方法是一样的都是物体各部分的重力和到转轴的距离的平方的乘积,对物体整体的积分。但是转动惯量的转动中心可以是空间任何一条轴、任何一个质点,而且电机扭矩的转动中心只能是电机的转动轴。
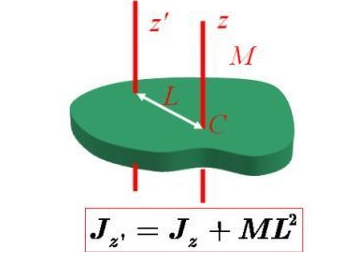
转动惯量(Moment of Inertia)是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字郑虚母I或J表示。在经典力学中,转动惯量(又称质量惯性矩,简称惯距)通常以I 或J表示,SI 单位为 kg·m²。
电机扭矩即电动机的输出扭矩,为电动机的基本参数之一。常用单位为N*m(牛*米)。
对于一个质点,I = mr²,其中 m 是其质量,r 是质点和转轴的垂直距离。转动惯量在旋转动力学中的角色相当于线性动力学中的质量,可形式地理解为一个物体对于旋转运动的惯性,用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。
转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大小)无关。形状规则的匀质刚体,其转动惯量可直接用公式计算得到。而对于不规则刚体或非均质刚体的转动惯量,一般通过实验的方法来进行测定,因而实验方法就显得十分重要。转动惯量应用于刚体各种运动的动力学计算中。
电机输出的扭矩与电动机的转速和功率有关。
P=T*ω(功率=扭矩*角速度)
T=9.55P/n 此卖岁公式为工程上常用的:扭矩;功率;转速三者关系的计算公式。
式中:T--扭矩(单位:N.M) 9.55-把它当作一常数吧(不必追究其来喊配燃源) P--电机的功率(单位:KW)
n--输出的转速(单位:转/分)
常数9.55的来历:T完成的功也就是电动机输出的功。
参考资料