用来三次方样条数据插值亏磨。具体解析如下:
一、语法及语法解析:
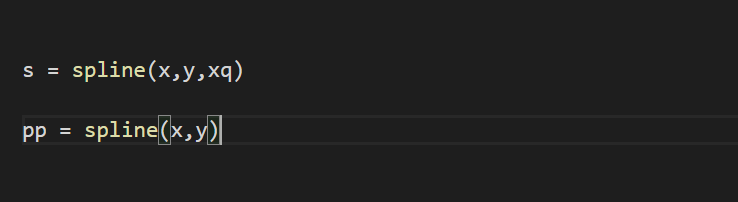
1、s = spline(x,y,xq) :
返回与 xq 中的查询点对应的插值 s 的向量。s 的值由 x 和 y 的三次样条插值确定。
xq是使用MATLAB画模拟信号图时,坐标轴的范围以及坐标点之间的间隔。这个间隔应该足够密集。
2、pp = spline(x,y) :
返回一个分段多项式结构体以用于 ppval 和样条实用工具 unmkpp。
二 、示例:
外插数据集以预测人口增长。
创建两个向量以表示从 1900 年至 1990 年的人口普查年 (t) 和相应的美国人口 (p)。
t = 1900:10:1990;
p = [ 75.995 91.972 105.711 123.203 131.669 ... 150.697 179.323 203.212 226.505 249.633 ];
外插并使用三次样条预测 2000 年的人口。
spline(t,p,2000),ans = 270.6060。
扩展资料:
MATLAB中的插值函数:
MATLAB中的插值函数为interp1,其调用格式为: yi= interp1(x,y,xi,'method') 。
其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量, 'method'表示采用的插值方法。
MATLAB提供的插值方法有几种:
1、'method'是最邻近插值, 'linear'线性插值;。
2、'spline'三次样条插值。
3、 'cubic'立方插值.缺省时表示线性插值。
所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
例子如下:
在一 天24小时内,从零点开始每间隔嫌拍2小时测得的芹空羡环境温度数据分别为12,9,9,10,18 ,24,28,27,25,20,18,15,13,推测中午12点(即13点)时的温度:
x=0:2:24;
y=[12 9 9 10 18 24 28 27 25 20 18 15 13];
a=13;
y1=interp1(x,y,a,'spline')
结果为: 27.8725。
参考资料: