a的值等空局坦于1。
计算过程:
因为函数f(x)连续,而且当x=0时,f(x)=a,当x不等于0是f(x)为连续的函数,所以如果要保持函数的连续性,则x趋近于0时的左右极限应该都要存在,而且需要等于x=0处的函数值。斗桐
lim(x趋近于0)(∫(0,x^3)sint/t)/(x^3)因为为0/0型,运用洛必达法则。
=lim(x趋近于0)sin(x^3)/x^3,运用无穷小量代换。
=lim(x趋近于0)x^3/x^3
=1=f(0)=a,所以得出a=1。
扩展资料:
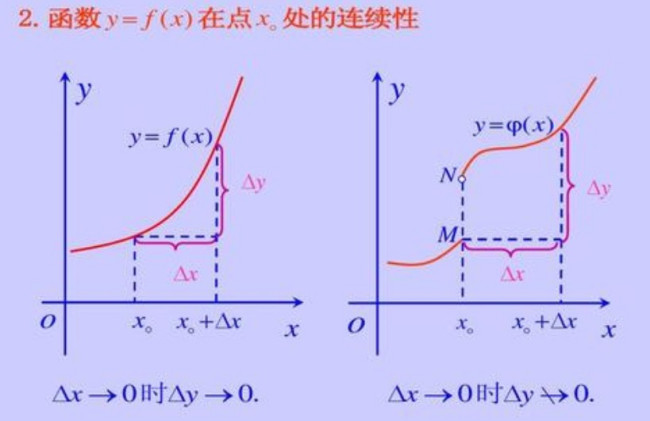
函数连续性的定理:
定理一 :在某点连续的有限个函数经有限次和、差、积、商(分母不为0) 运算,结果仍是一个在该点连续的函数。
定理二 :连续单调递增 (递减)函数的反函数,也连续单调递增 (递减)。
定理三 :连腊饥续函数的复合函数是连续的。
闭区间上的连续函数具有一些重要的性质:
1、有界性,闭区间上的连续函数在该区间上一定有界。
2、最值性,闭区间上的连续函数在该区间上一定能取得最大值和最小值。
3、介值性,若f(a)=A,f(b)=B,且A≠B。则对A、B之间的任意实数C,在开区间(a,b)上至少有一点c,使f(c)=C。
4、一致连续性,闭区间上的连续函数在该区间上一致连续。
当x趋近于0的时候有以下几个常用的等价无穷小的公式:
1、sinx~x、tanx~x、arcsinx~x、arctanx~x、1-cosx~(1/2)*(x^2)~secx-1。
2、(a^x)-1~x*lna [a^x-1)/x~lna]。
3、(e^x)-1~x、ln(1+x)~x。
参考资料来源:百度百科-连续函数