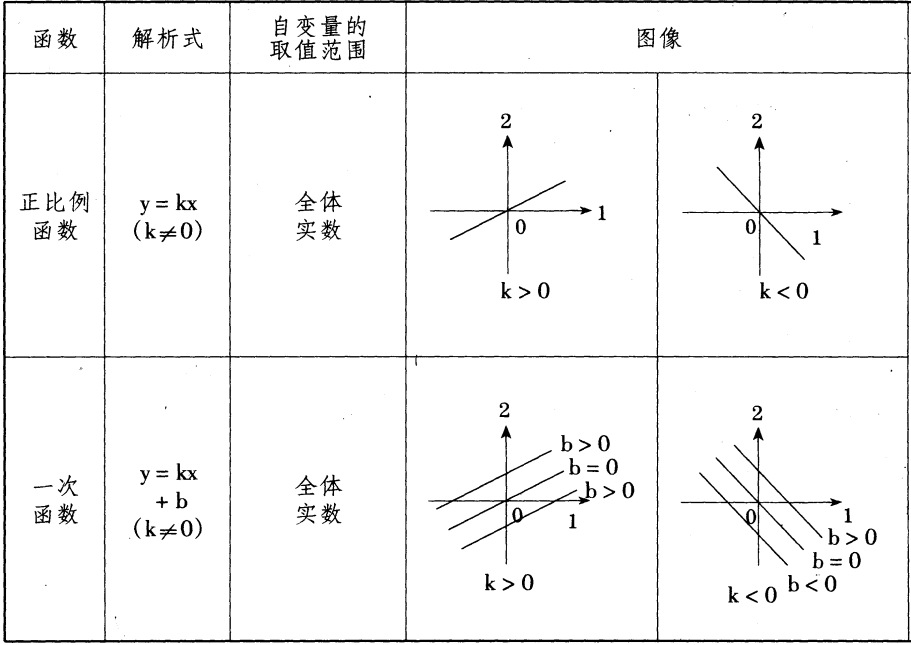
一次函数的单调性是函数曲线只有一个方向性,单调无改变。
设y=kx+b(k0),则当k>0时,y随亮裂者x的增大而增大;当k<0,y随x的增大而减小。
函数性质:
1、y的变化值与对应的x的变化值成正比例,比值为敬薯k。
即:y=kx+b(k≠0)(k不等于0,且k,b为常数)。
2、当x=0时,b为函数在y轴上的交点,坐标为(0,b)。
当y=0时,该函数图象在x轴上的交点坐标为(-b/k,0)。
3、k为一次函数y=kx+b的斜率,k=tanθ(角θ为一次函数图象与x轴正方向夹角,θ≠源肢90°)。
4、当b=0时(即y=kx),一次函数图象变为正比例函数,正比例函数是特殊的一次函数。
扩展资料
当平面直角坐标系中两直线平行时,其函数解析式中k的值(即一次项系数)相等;
当平面直角坐标系中两直线垂直时,其一次函数斜率的乘积=-1。
关于平面直角坐标系中两直线垂直时,其函数解析式中K值互为相反数的证明:
2个函数互相垂直,但若直接证明,存在困难,不易理解,如果平移平面直角坐标系,使这2个函数的交点交于原点,就会更简单。
可以设这2个函数的表达式分别为:y=ax,y=bx。
参考资料来源:百度百科-一次函数