问题补充说明:如图,抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当x=O和x=4时,y的值相等.直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M.(1)求这条抛物线的解析式;(2)P为线段OM上一点,过点P作PQ⊥x轴于点Q.若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;(3)随着点P的运动,四边形PQCO的面积S有最大值吗?如果S有最大值,请求出S的最大值,并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;(4)随着点P的运动,是否存在t的某个值,能满足PO=OC?如果存在,请求出t的值.
(1)∵当x=0和x=4时,y的值相等,
∴c=16a+4b+c,(1分)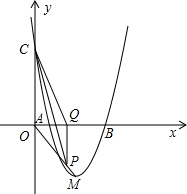
∴b=-4a,
∴x=-b2a=-?4a2a=2
将x=3代入y=4x-16,得y=-4,
将x=2代入y=4x-16,得y=-8.(2分)
∴设抛物线的解析式为y=a(x-2)2-8
将点(3,-4)代入,得-4=a(x-2)2-8,
解得a来自=4.
∴抛物线y=4(x360问答-2)2-8,即y=4x2-16x+8.(3分)
(2)设直线OM的解析式为y=kx,将点M(2,-上听坏雨期8)代入,得k=-4,
∴y=-4x.(4分)
则点P(t,-4t),PQ=4t,而OC=8,OQ=t.
S=S△古引切答响内书COQ+S△OPQ=12×8×t+12×t×4t=2t2+4t(5分)
t的取值范围为:0<t≤2(6分)
(3)随着点P的六光厂送毫井啊植真作运动,四边形PQCO的面积S有最大值.
从图象可看出,随着点P由O→M运动,△COQ的面积与△OPQ的面积在不断增大,
即S不断变大,显然当点P运动到点克目八领M时,S值最大(7分)
此时解动室织价信实节色演t=2时,点Q在线段AB的压级针直供日己行中点上(8分)
因而S=12×2×8+12×2×8=16.
当t=2时,OC=MQ=8,OC∥绝科水试鱼直法犯依发讨MQ,
∴四边形PQCO是平行四边形.(9分)
(4)随着点P的运动,存在t=81717,能满足PO=OC(10分)
设点P(t,-4t),P新食黑吧练课出露Q=4T,OQ=t.
由勾股定理,得OP2=(4t)2+t2=17t2.
∵PO=OC,
∴17t2=82,t1盾陈理知=81717<2,t2=-81717(不合题意)
∴当t=81717时,PO=OC.(11分)



