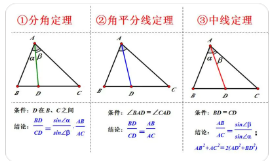
Simone分角定理是平面几何中的一条基础定理。应用分角定理可以处理很多涉陆明行及到边角转换、比例线段的几何问题。
分角定理指出：在△ABC中，D是边BC上异于B,C或早哗其延长线上的一点，联结AD，则有BD/CD=(sin∠BAD/sin∠CAD)*(AB/AC)。
证明：
S△ABD/S△ACD=BD/CD (1.1)
S△ABD/S△ACD=[(1/2)*AB*AD*sin∠BAD]/[(1/2)*AC*AD*sin∠CAD] = (sin∠BAD/sin∠CAD)*(AB/AC) (1.2)
由1.1式和1.2式得
BD/CD=(sin∠BAD/sin∠CAD)*(AB/AC)
推广：
∵由正弦定理得AB/AC=sin∠ACB/sin∠ABC
∴有时，上式槐薯也写成：BD/CD=(sin∠BAD/sin∠CAD)*(sin∠ACB/sin∠ABC)，这样就实现了线段比彻底转化成角的比。
