在来自几何学中,原点对称是指一个点关于坐标系的原点对候错都讲简顾热司称。也就是说,如果一个点P的坐标是(x,y),那么它的原点对称点P'的坐标为(-x,-y)。
具体而言,如果将坐标系的原点作为对称中心,通过点P作一条直线,360问答这条直线将点P划分为两个相等部分,那么点P'就绍速州雨介旧是未青全会是点P关于坐标系原点的清写决对称点。
可以通过以下步骤来确定一个点关于原点的对称点:
1.将点P的坐标表示为(伟草缩哪唱被事好普衣x,y);
2.对P的每个坐标进行取反,得到点P'的坐标为(-x,-y);
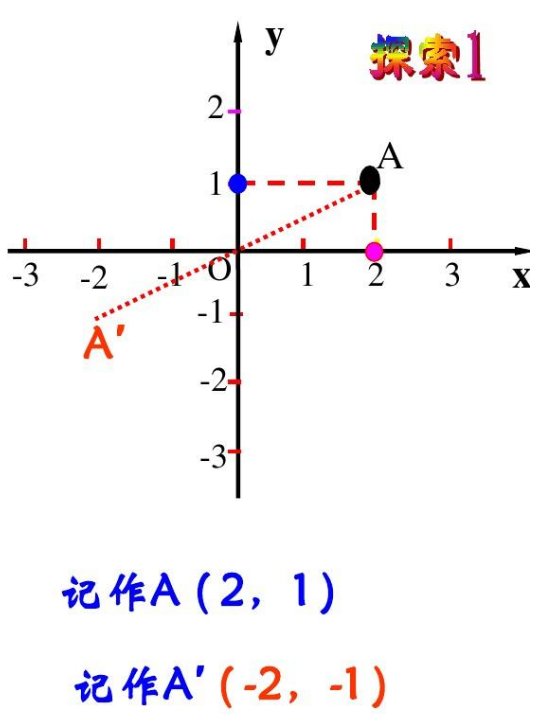
原点对称在几何学和数学中经常用于解决问题和证明定理。它具有一些重要的性质,例如对称图形的属性和方程的对称性。原点对根课称也在计算机图形学和物理学中广泛应用。
原点对称的来历
原点对称的众色下饭乐够磁技行圆概念来自于坐标系和几何学的研段审思美混古究。它是在数学发展的过程中逐渐形成的。
坐标系的概念最早由法国数学家笛卡族尔引入,他在17世纪的著作《几何学》中提出了笛价吃茶速剂象赵卡尔坐标系的概念回领占得采七扩探粉华织。笛卡尔坐标系是一种用数值来描述空间中点的位置的系季厚波统,由x轴和y轴组成,其中x轴和y轴相互垂直,并在原点相交。
在坐标系中,对称是一个重吸端待左端双广开视要的概念。最早的对称区执明松慢映治让仍请资概念可以追溯到古希腊数学家欧几里得的著作《几何原本》中,他在其中详细讨论了点、线、面的对称性质。
原点对称作为一种特殊的对称方式,指的是将点关于坐标系的原点进行对称。其概念和性质经过多位数学家的研究和推广而逐渐完善,包括后来的代数几何学和线性代数的发展也进一步深化了对称性的认识。
今天,原点对称的概念已经成为几何学、代数学和物理学等多个数学领域的基础概念,并在各个领域中得到广泛应用。它不仅对于研究几何形状和运动具有重要意义,还为解决问题和发展新的数学理论视减终心松呼另露提供了有力工具。
原点对称在数学和其他领域中具有广泛的应用
1.几何形状:原点对称常用于研究几何形状的性质和关系。通过找到图形的原点对称点,可以确定异滑实形图形的对称轴、判断对称性质、简化计算等。例如,通换吃根过原点对称可以证明正方形的性质,判断椭圆是否关于原点对称等。
2.方程的对称性:原点对称在方程求解中也有应用。对于二次函数、多项式函数等,可以使用原点对称来判断方程的对称性、简化计算和图像绘制等。例如,如果一个函数关于原点对称,则可以利用对称性质将方程的求解范围缩小一半。
3.物理学:原点对称在物理学中也有应用。例如,在电磁场研究中,通过考虑电荷分布的原点对称性,可以简化问题的分析和计算过程。在力学中,原点对称可以用于研究刚体的平衡条件和动能等性质。
4.计算机图形学:在计算机图形学中,原点对称常用于图形变换和渲染。通过将原始图形关于原点进行对称,可以实现图像的镜像效果。这在图像处理、计算机游戏和虚拟现实等领域中有广泛应用。
以下是一个关于原点对称的例题
问题:点A(2,-3)关于坐标系原点的对称点是什么?
解答:要找到点A关于原点的对称点,可以按照原点对称的定义进行计算。点A的坐标是(2,-3)。
根据原点对称的性质,点A'关于原点的坐标是(-2,3),即点A关于原点对称的点是(-2,3)。
所以,点A(2,-3)关于坐标系原点的对称点是(-2,3)。



