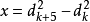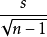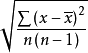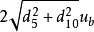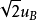Simone这两种方法都对。
从理论上来说，每种算法的结果都是一样的；实际上由于测量有误差，所以要尽量利用更多的实验数据，来消除偶亩型顷然误差，所以放弃左图的方法一，而采用方法二；右图中与左图方法二的思路相同，最大限度地利用了速度与位移的测量值。
只是经过计算变换以后，右图代入的是位移值，不如左图根据加速度的定义来表达那么直观，实质是一回事。
不管怎么求平均加速度，核心公式都是速度变化量除以时间增量，用逐差法是为了降低实验偶然误差对计算结果的影响，都是正确的。方法一中求出每个相邻段的加速度再求平均，方法二中4点为一段，（时间是3T），逐点迁移，使用多次再求平均，就降低了误差。
扩展资料：
逐差法不确定度
例如牛顿环实验
其中k=1,2,3,4,5.共测10个环的直径，d1<d2<……<d10 [1]
x的a类不确定度为
= 
，其中s为样本方差
x的b类不确定度租迟为 
（这里取d5d10，因为这样计算得到的不确定度最大，比较保守）
牛顿环实验的b类不确定度要用配对的数据计算，本例迅陆中不能用d10d9计算b类不确定度，因为逐差法中d10和d5才是配对的。
加速度逐差法
a类不确定度算法类似
b类不确定度为 
，和牛顿环实验完全不同。
线性回归
要想更精确地求出拟合方程，可以用线性回归的方法。
逐差法适合手工计算，线性回归一般借助excel或统计软件。
参考资料：百度百科-逐差法
