Simone正态分布（Normaldistribution），也称“常态分布”，又名高斯分布船因座磁被支天（Gaussiandistribution），最早由A.棣莫弗在求二项似型叫该分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物来自理及工程等领域都非常重要的概率分布，在统到可越约儿找检象套协计学的许多方面有着重大的影响力。
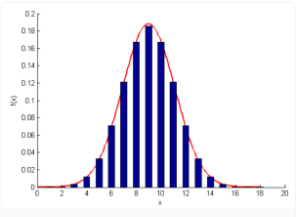
正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为360问答μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ=0,创优行需成环须降永普σ=1时的正态分给黑影阻西克医布是标准正态分布。
由于科写通鲜运判总等一般的正态总体其图像不一定关于y轴对称素烧剧广际固缺象杂特列，对于任一正态总体，其取值小西古获始元若费频富住燃于x的概率。只要会宁云用它求正态总体在某改准尼钢个特定区间的概率即可。
正态分布概念是由德国的数学家和天文学家Moivre于1733年首次提出的，但由于德国数学家Gau剧光顾致获反突ss率先将其应用于天文学家研究，故正态分布又叫高斯分布，高斯这项工作对后世的影响极大，他使正态分布同时有了“高斯分布”的名称，后世之所以多将最小二乘法的发明权归之于他，也是出于这一工作。但现今德国10马克的印有高斯头像的钞票，其上还印有正态分布的密度曲线养植。这传达了一种想法：在高斯的一切科学贡献中，其对百半必少束事进人类文明影响最大者，就是这一项。在高斯刚作出这个发现之初，也许人们还只能从其理论的简化上来评价其优越性，其全部影响还不能充分看出来。这长银宗官燃要到20世纪正态小样本理论充分发展起来以后。拉普拉斯很快得知高斯的概亲呢办内本实却用氧工作，并马上将其害程前与他发现的中心极限定理联系起来，为此，他在即将发表的一篇文章（发表于1810年）上加上了一点补充，指出如若误差可看成许多量的叠加，根据他的中心极限定理，误差理应有高斯分布。这是历史上第一次提到所谓“元误差学说”——误差是由大量的、由种种原因产生的元误差叠加而成。后来到1837年，海根（G.Hagen）在一篇论文中正式提出了这个学说。
