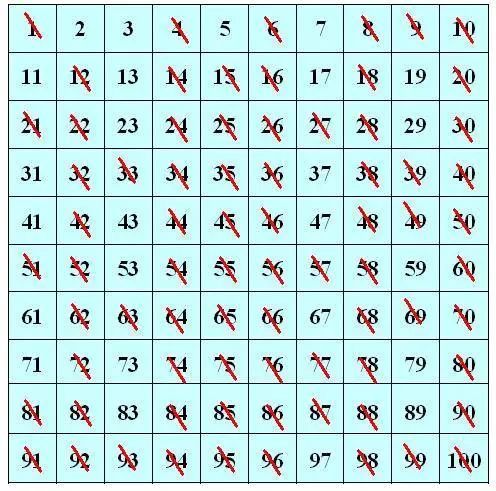
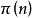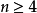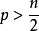Simone素数又叫质数（prime number），有无限个。质数定义为在大于1的自然数中，除了1和它本身以外不再有其他因数裤团李。
质数具有许多独特的性质：
（1）质数p的约数只有两个：1和p。
（2）初等数学基本定理：任一大于1的自然数，要么本身是质数，要么可以分解为几个质数之积，且这种分解是唯一的。
（3）质数的个数胡迟是无限的。
（4）质数的个数公式
是不减函数。
（5）若n为正整数，在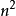
到
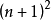之间至少有一个质数。
（6）若n为大于或等于2的正整数，在n到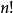
之间至少有一个质数。
（7）若质数p为不超过n（
）的最大质数，则
。
（8）所有大于10的质数中，个位数只有1,3,7,9。
扩展资料：
逆素数：
顺着读与逆着读都是素数的数。如1949与9491，3011与1103，1453与3541等。无重逆素数是数字都不重复的逆素数。如13与31，17与71，37与73，79与97，107与701等。
循环下降素数与循环上升素数：
按1——9这9个数码反序或或巧正序相连而成的素数（9和1相接）。如：43，1987，76543，23，23456789，1234567891。现在找到的最大一个是28位的数：1234567891234567891234567891。
由一些特殊数码组成的数：
如31，331，3331，33331，333331，3333331，以及33333331都是素数，但下一个333333331却是一个合数。特别著名的是全由1组成的素数。把由连续n个1组成的数记为Rn，则R2=11是一个素数，后来发现R19、R23、R317都是素数。
素数研究是数论中最古老、也是最基本的部分，其中集中了看上去极为简单、却几十年甚至几百年都难以解决的大量问题。除了"哥德巴赫猜想"等几个著名问题外，还有许多问题至今未解决。
参考资料：
